METEOR FLIGHT THROUGH THE ATMOSPHERE
INTRODUCTION
 The observation of a meteor during its transient existence can provide a wealth of information about the meteoroid and the atmosphere through which it travels. In the late 16th century, observations of meteors from separated sites gave proof that the Earth's atmosphere extended to a height of at least 100 kilometres. Air densities and temperatures at these altitudes were derived from photographic records in the first half of the 20th century. Later research provided insights into the nature of the particles which produced the meteor phenomenon.
The observation of a meteor during its transient existence can provide a wealth of information about the meteoroid and the atmosphere through which it travels. In the late 16th century, observations of meteors from separated sites gave proof that the Earth's atmosphere extended to a height of at least 100 kilometres. Air densities and temperatures at these altitudes were derived from photographic records in the first half of the 20th century. Later research provided insights into the nature of the particles which produced the meteor phenomenon.
The model presented here simulates the flight of a meteoroid through the upper atmosphere using the equations of classical meteor ablation theory. This theory was developed by many people, including Fred Whipple and Ernst Opik. Although the theory has some definite limitations, it not only provides a good insight into the decleration, mass loss and visible radiation of the meteoric process, it also forms the basis of more extended theories that deal with the crumbling particles that we know form the bulk of meteoroids producing visual meteors.
This model traces the variation of the meteoroid velocity, decleration, mass and visual radiation with time. By varying the appropriate model parameters such as initial conditions or the atmospheric environment, the effect of each can be readily evaluated. The model is valid not only for the Earth but can also be used for other bodies with an atmosphere such as Mars.
The model can also be adapted to the reentry of orbital space debris.
CLASSICAL METEOR ABLATION THEORY
When a meteoroid first encounters a significant atmosphere it undergoes collisions with the air molecules. By this process momentum is transferred from the meteoroid to the air. The resultant deceleration of the meteoroid is proportional to the cross-sectional area it presents to the direction of travel and to the drag coefficient. The cross-sectional area is dependent on the on the shape of the body, its physical orientation and whether or not it si rotating.
High in the atmosphere, where there are few air molecules, the drag coefficient lies close to one. All molecules within the cross-sectional forward projection undergo collisions. Lower down, where the atmospheric density becomes greater , an air-cap forms around the incadescent body, shielding it in part from some of the air column. This effectively reduces its effective cross-section, and the drag coefficient drops to around one half (0.5).
The kinetic energy of the meteoroid is continually reduced as it traverses the atmosphere to lower altitudes. This energy is converted into heat, light and energy of ionisation. Most of the energy is in the form of heat which causes vapourisation of surface material from the meteoroid - a process known as ablation. The mass of the meteoroid is reduced at a rate proportional to the loss of kinetic energy. Two parameters are important in this transfer of energy: the heat of ablation of the meteoroid material, and the heat transfer coefficient. This latter quantity is a measure of the efficiency of the collision process in converting kinetic energy to heat.
The visual power that is radiated by the meteor is proportional to the loss of kinetic energy of the ablated material. The proportional constant is termed the luminous efficiency, and this has a strong dependence on the nature of the meteoroid. The visual power can be transformed into an absoluted magnitude through a simple experimentally derived formula. By definition the absolute magnitude of a meteor is the observed magnitude at a distance of 100 km. The apparent magnitude then includes the actual meteor-observer distance ratio as a correction term.
THE METEOR EQUATIONS
As the meteoriod encounters significant atmosphere, its momentum is decreased through collisions with air moleculs. This momentum tranfer can be quantified with the help of Newton's second law of motion giving the Resistance or Drag Equation:
dv/dt = ( Γ A ρa v2 ) / ( m1/3 ρm2/3 )
where
v is the speed of meteoroid ( m s-1 )
dv/dt is the deceleration of the meteoroid ( m s-2 )
Γ is the drag coefficient
A is the meteoroid shape factor
m is the meteoroid mass ( kg )
ρm is the meteoroid density ( kg m-3 )
ρa is the atmospheric density ( kg -3 )
A second equation, the Differential Mass Equation, is derived by assuming that the rate of loss of mass is proportional to the kinetic energy transferred to the mass of air intercepted by the meteoroid:
dm/dt = ( Λ A ρa v3 m2/3 ) / ( 2 ζ ρm2/3 )
where
Λ is the heat transfer coefficient
ζ is the heat of ablation of the meteoroid
The visual power radiated by the meteoroid is given by:
where ΤI is the luminous radiation efficiency. This may be converted into a rough apparent visual magnitude for a ground-based observer through the empirical relation:
Mv = 6.8 - 2.5 log10( I ho2 / h2 )
where ho is a reference height of 100 km The squared altitude ratio takes into account the apparent magnitude change due to the distance from the observer, but is only correct for an observer directly below the meteor. Absolute magnitude is obtained by setting h = ho.
The table below lists typical initial values for the above parameters and a few others used in the computer implementation of the model.
| Parameter | Description | Program Variable | Typical Initial Values |
|---|
| A |
Meteoroid shape factor |
A |
0.8 - 1.2 |
| Γ |
Drag coefficient |
G |
0.5 - 1.0 |
| ρm |
Meteoroid density |
D |
500 - 8000 kg m-3 |
| ζ |
Meteoroid heat of ablation |
H1 |
(0.1-10) x 106 J kg-1 |
| Λ |
Heat transfer coefficient |
H0 |
0.5 - 6 |
| ΤI |
Luminous efficiency |
L |
2x10-2 - 2x10-4 |
| v |
Meteoroid velocity |
V |
11,000 - 72,000 m s-1 |
| m |
Meteoroid mass |
M |
~10-8 - 1000 kg |
| Z |
Entry zenith angle |
Z |
0o - 99o |
| h |
Meteoroid height |
H |
130 - 180 km |
ATMOSPHERIC DENSITY
Atmospheric density varies with altitude, and it also varies to a lesser extent with location (latitude and longitude), time (season and hour of the day), and a few other minor factors.
And of course it varies enormously from planet to planet. With the appropriate expression for air density this model can
be used to compare the differences in meteors that occur on Mars and the Earth.
The accuracy of the expression to be used for air density really depends on the purpose for which the model is being used. If the model is only used to illustrate the basic nature of meteor ablation a simple exponential expression of the form ρ = ρ0 exp(-h/H) is quite
adequate. This assumes that the atmosphere is isothermal and homogeneous (composition does not change with altitude). Suitable expressions for the Earth and for Mars are:
Earth: ρ = 1.25 exp( - h / 7000 )
Mars: ρ = 0.0156 exp( - h / 10000 )
where the height above the surface (h) is in kilometres and the density is in kilogram per cubic metre. For meteors on the Earth only altitudes below 150 km need to be considered.
A discussion of atmospheric density models can be found in
Atmospheric Density Models. This contains a more accurate expression for the density of the Earth's atmosphere from the surface to 180 km altitude. This is given by the expressions:
log10(ρ) = polyfn( h )
where
polyfn(h) = a0 + a1*h + a2*h2 + a3*h3 + a4*h4 + a5*h5 + a6*h6 + a7*h7
with the coefficients a0 to a7 given in the above web reference.
This model is still an average value over many different locations and times, but it will give a more realistic meteor ablation model for the Earth.
IMPLEMENTATION
The model described by the above equations can be implemented
by a simple QBASIC program as shown below.
'METFLITE.BAS Terrestrial Atmospheric Meteor Flight
'input data
CLS
PRINT "METEOR FLIGHT"
INPUT " Initial Mass (kg)"; imass
INPUT " Density (kg/m^3)"; mdens
INPUT " Speed at Entry (km/s)"; ivelk
INPUT " Zenith Angle (deg)"; zadeg
'convert inputs
mm = imass 'current meteoroid mass (kg)
cza = COS(zadeg * dr) 'cosine of zenith angle
vel = ivelk * 1000 'current meteoroid velocity (m/s)
'parameters
pi = 3.14159
dr = pi / 180 'degrees to radians
Asf = 1.2 'meteoroid shape factor
Le = .001 'luminous efficiency
Dc = 1 'drag coefficient
Htc = .15 'heat transfer coefficient
Ha = 3000000 'heat of ablation (J/kg)
'loop values
h = 150000 'starting height (m)
t = 0 'time variable - initially zero seconds
dt = .0001 'time step in seconds
tprint = 1.5 'first print time (secs)
PRINT
PRINT " TIME HEIGHT SPEED DECEL MASS VISUAL"
PRINT " (S) (KM) (KM/S) (M/S/S) (%) MAG"
f$ = "##.## ###.# ##.# ###### ###.# ###.# &"
'computational loop
DO
rho = 1.3 * EXP(-h / 7000) 'atmospheric density (kg/m^3) at height h km
'now compute meteoroid deceleration and mass loss
decl = Dc * Asf * rho * vel * vel / ((mm ^ .33333) * (mdens ^ .66667))
ML = Htc * Asf * rho * vel * vel * vel * ((mm / mdens) ^ .66667) / (2 * Ha)
dv = decl * dt 'velocity decrement = decleration * time_increment
dm = ML * dt 'mass decrement = mass_loss * time_increment
t = t + dt 'increment time
h = h - vel * dt * cza 'compute new height
vel = vel - dv 'new veloicty
mm = mm - dm 'new mass
Iv = .5 * Le * ML * vel * vel 'visual power (watts)
Mv = 6.8 - 2.5 * LOG(Iv * (100000 / h) ^ 2) / 2.303 'visual magnitude
fracmass = mm / imass 'fractional mass remaining
IF t > tprint THEN 'print loop
IF Mv < 5 THEN vis$ = "vis" ELSE vis$ = "" 'is meteor visible?
PRINT USING f$; t; h / 1000; vel / 1000; decl; fracmass * 100; Mv; vis$
tprint = tprint + .5 'increment print time
IF vel < 1000 THEN EXIT DO 'exit if velocity < 1 km/sec
END IF
LOOP
END
|
This program uses a simple exponential approximation for atmospheric density. It produces the output:
METEOR FLIGHT
Initial Mass (kg)? 0.001
Density (kg/m^3)? 3500
Speed at Entry (km/s)? 20
Zenith Angle (deg)? 45
TIME HEIGHT SPEED DECEL MASS VISUAL
(S) (KM) (KM/S) (M/S/S) (%) MAG
1.50 120.0 20.0 1 100.0 9.7
2.00 110.0 20.0 4 99.9 8.0
2.50 100.0 20.0 17 99.7 6.2
3.00 90.0 20.0 71 98.8 4.5 vis
3.50 80.0 19.9 297 95.0 2.7 vis
4.00 70.1 19.6 1245 80.7 1.1 vis
4.50 60.6 18.2 5197 42.0 0.2 vis
5.00 52.6 13.0 16377 5.5 1.9 vis
5.50 48.1 5.5 9838 1.0 7.0
6.00 46.2 2.6 3170 0.7 10.9
6.50 45.2 1.6 1339 0.7 13.5
7.00 44.6 1.1 699 0.7 15.4
7.50 44.1 0.8 418 0.7 16.9
|
All of the parameters of the model can be changed to show what
effect each has. Other parameters may be output. Kinetic energy might be an appropriate quantity to add to the list of output parameters.
EXPLORING THE MODEL
Examination of the model output can give an idea of the basics
of meteoroid ablation:
(1) Notice the extremely high decleration experienced by the meteoroidas its kinetic energy is reduced. The maximum shown in the above example is 1600g (ie 1600 times the gravitational acceleration)
(2) A one gram meteoroid typically produces a zeroth magnitude meteor.
(3) The meteor is visible for 2 seconds - in fact the typical visual meteor (which has a magnitude less than 0) will be visible for less than a second.
(4) The ablation process consumes mass in preference to speed. Only when two thirds of the mass is gone does the speed really start to significantly reduce.
We need to plot some graphs to show the effect of varying different meteor parameters.
Meteoroid velocity
The curve below shows the effect of varying the meteoroid velocity, keeping mass and density constant.
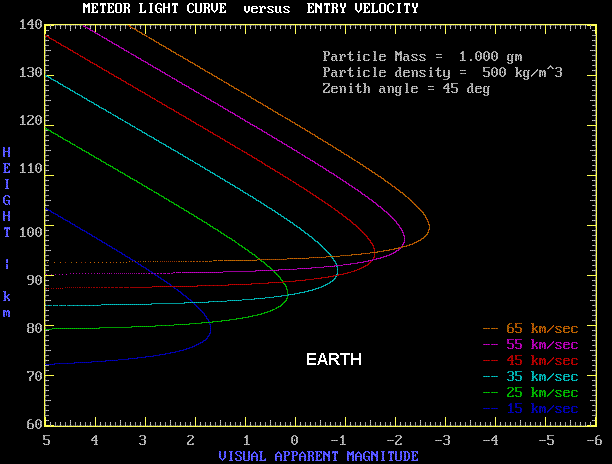
Higher velocity meteoroids start to ablate earlier in the entry process. They also produce brighter meteors per unit mass.
The next curve has the same meteoroid parameters as above, but translates the entry to Mars.
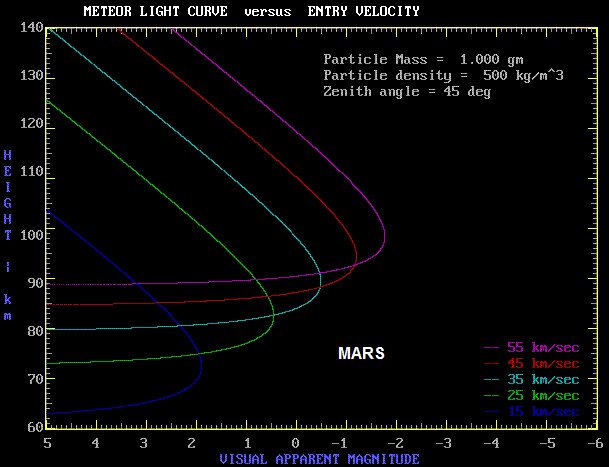
These curves are remarkably similar to those for the Earth. The ablation occurs at a slightly lower altitude on Mars than on Earth. This is because although the Martian surface atmosphere density is much lower, the scale height is larger on Mars (because of lower gravity) and thus the densities of the two atmospheres is not that different at high altitudes. Note that a curve for a velocity of 65 km/sec is missing in the Martian plot. This is because Mars has a slower orbital velocity than Earth and because solar escape velocity is lower at the more distant Martian orbit.
The real difference in the entry process for the two planets is noted for the larger meteoroids. This is discussed in Martian Meteorites.
Meteoroid Density
The curve below shows the effect of varying the meteoroid density, keeping mass and velocity constant.
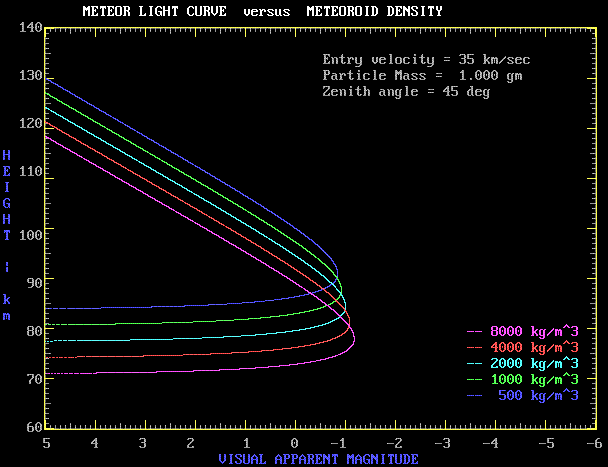
Meteoroids with larger densities will be more compact objects. These travel further down into the atmosphere during ablation and produce a slightly brighter meteor.
Meteoroid Mass
The curve below shows the effect of varying the meteoroid mass, keeping velocity and density constant.
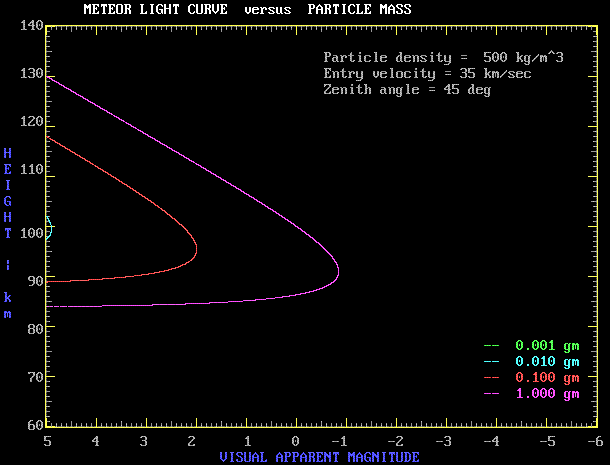
The predominent effect is on meteor brightness. We can see that a cometary meteor (low density - 500 kg/m3) with a meteoroid mass less than 10 mg will not be visible.
There is a minor decrease in height of maximum brightness as the meteoroid mass increases.
There are many more such plots that can be made to learn about the meteor ablation process.
THEORY AND OBSERVATIONS
How does the above theory correspong to reality? Consider the three light curves below by L Jacchia as reproduced by Hawkins (1964).
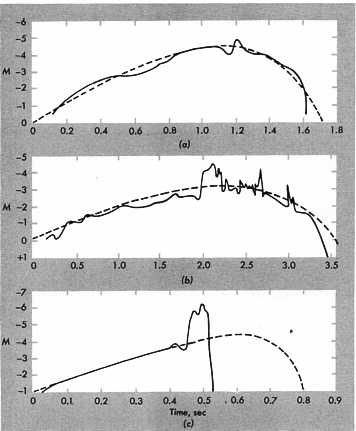
The solid lines are the observed light curves for three bright meteors, whereas the dashed lines are the classical ablation model fits to best match the observed curves. The velocities of the meteors are respectively (a) 36 km/s, (b) 25 km/s and
(c) 69 km/s.
The model fits the observed curve in (a) quite well, except
at the very end of the flight. The situation is (b) is still not too bad but shows substantial brightening near time of maximum light, whereas in (c), the model fails totally before the time of maximum light.
The resolution of the problem is that meteoroids don't always remain as one smoothly ablating mass. The enormous decleration experienced in meteor flight may cause the meteoroid to implode or fragment. This is particularly the case for a cometary meteor where the meteoroid is of a low density rather fragile material. This produces many pieces, each of which then undergoes ablation as separate entity. This results in more light being produced than for a single object. In the case (c), the object has undergone terminal implosion into many pieces, creating a flare which quickly fades away.
In summary, meteoroid fragmentation produces shorter trails,
wider trails and a brighter meteor. Fragmentation is often not a single event but something that occurs intermittently along the reentry path.
As long as the meteoroid remains intact, we have every reason to believe that classical ablation theory provides a close estimate to the process that occurs in meteor flight.
Extension of the theory to include fragmentation can demonstrate the features of this process.
SPACE DEBRIS REENTRIES
This theory not only applies to meteoroids entering a planetary atmosphere, but is also applicable to the reentry of space debris.
In the reentry of orbital space debris the zenith angle is around 89 degrees. That is, the debris object enters at nearly grazing incidence to the atmosphere. Such an object has a velocity around 7 to 8 kilometres per second, lower than any meteoroid (which has a minimum velocity of 11 km/s - equal to the escape velocity of the Earth).
Gravity is much more important in this case, and the reentering object will travel a substantial distance around the Earth during the ablation process. The above model thus needs to incorporate the force of gravity into the equations.
This is done, and the results of reentering objects are discussed in Modelling a Space Debris Reentry.
REFERENCES
E Opik, Physics of Meteor Flight in the Atmosphere, Interscience Publishers (1958)
DWR McKinley, Meteor Science and Engineering, McGraw-Hill (1961)
Gerald S Hawkins, Meteors, Comets and Meteorites, McGraw-Hill (1964)
ADDITIONAL NOTES
1 The Meteoroid Shape Factor
When a large piece of space debris reenters the Earth's atmosphere we often have knowledge of its shape and size. This is not so in the case of a meteoroid. In both cases it is the effective cross-section of the body in the direction of travel that is the important parameter in the deceleration process.
Because of our ignorance of this parameter for a meteoroid it is conventional to define a dimensionless shape parameter
A where:
is the effective cross-sectional area of the meteoroid.
The figure below shows the values of A for various shapes.
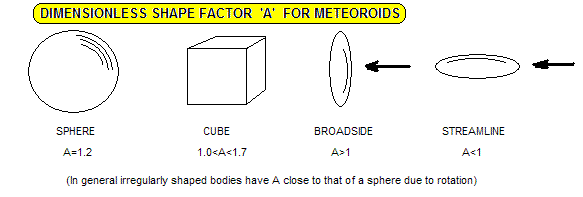
All these are close to unity, and this value is normally used in meteor ablation theory.
 Australian Space Academy
Australian Space Academy
 The observation of a meteor during its transient existence can provide a wealth of information about the meteoroid and the atmosphere through which it travels. In the late 16th century, observations of meteors from separated sites gave proof that the Earth's atmosphere extended to a height of at least 100 kilometres. Air densities and temperatures at these altitudes were derived from photographic records in the first half of the 20th century. Later research provided insights into the nature of the particles which produced the meteor phenomenon.
The observation of a meteor during its transient existence can provide a wealth of information about the meteoroid and the atmosphere through which it travels. In the late 16th century, observations of meteors from separated sites gave proof that the Earth's atmosphere extended to a height of at least 100 kilometres. Air densities and temperatures at these altitudes were derived from photographic records in the first half of the 20th century. Later research provided insights into the nature of the particles which produced the meteor phenomenon.






 Australian Space Academy
Australian Space Academy