LEO parameters

ORBITAL PARAMETERS

LOW EARTH CIRCULAR ORBITS

LEO circular orbit A circular orbit is mathematically the simplest orbit, although it can be difficult to achieve exactly in practice. Only one parameter is needed to specify the size of the orbit, and that is the radius r, the constant distance from the centre of the Earth to the satellite.

If the radius of the Earth is denoted by Re, then the altitude or height of the orbit (and the satellite) above the Earth's surface is h = r - Re.

Unfortunately for our simplicity, the radius of the Earth is not a constant, varying from 6357 km at the poles to 6378 km at the equator. If our satellite has a low inclination (ie it spends most of its time near the equator), then we might use the equatorial radius. Otherwise we could use the mean radius of 6371 km. Of course, for high accuracy applications we need to consider the varying shape of the Earth at each point beneath the satellite's orbit.

If we know the period of the satellite (the time it takes to make one complete orbit around the Earth) we can compute its height, and vice versa. We can also compute its orbital velocity (v) and a quantity known as its mean motion, the number of orbits it completes in one day.

Isaac Newton provided the formulae we need for these calculations. Starting with the famous second law (N2) of motion F = ma where F is the force on the satellite, m is its mass and a is its acceleration.

Newton's law of gravitation F = G M m / r² is the required force that the Earth exerts on the satellite.

A body moving in a circle is actually being accelerated toward the centre of the circle (by the Earth's gravitational force). The acceleration is referred to as the centripetal (directed towared the centre) acceleration, and the force that produces the acceleration is known as the centripetal force.

The magnitude of the acceleration is given by a = v² / r .

If we substitute for the force on the left hand side of N2 and the acceleration on the right hand side we end up with:

where

We now note that the mass of the satellite (m) disappears from the equation, and we are left with an expression relating the orbital velocity to the orbital radius:

v = √ ( G M / r ) The orbital period (T) may be computed by dividing the distance travelled in one orbit by the velocity. The former quantity is the circumference of the circle.

T = 2 π r / v which after substitution for v becomes:

Lastly, the mean motion (n) of the satellite, which is defined as the number of orbits traversed in one complete day which is 86400 seconds long, given by:

n = 86400 / T Note that with the exception of n, all quantities are strict SI units. Distances are in metres, velocities in metres/sec and times in seconds. The exception, the mean motion, is in revolutions per day.

In this system of units, the values for the gravitational constant and the mass of the Earth is given as:

^-11

^-1

^-2

²⁴

It is interesting to note that the uncertainty in the measured value for G is larger than the uncertainty in the measurement of the product of G times M, which is given as:

¹⁴

^-2

A table of values computed from the above formulae is shown below. Note that the units have been converted into the more typically used quantities before display.

               LEO CIRCULAR ORBIT PARAMETERS

           Height   Velocity   Period   Mean Motion
            (km)     (km/s)    (mins)    (revs/day)

             200      7.79       88.4      16.30
             300      7.73       90.4      15.93
             400      7.67       92.4      15.58
             500      7.62       94.5      15.24
             600      7.56       96.5      14.92
             700      7.51       98.6      14.60
             800      7.46      100.7      14.30
             900      7.40      102.8      14.00
            1000      7.35      105.0      13.72
            1100      7.30      107.1      13.44
            1200      7.26      109.3      13.18
            1300      7.21      111.4      12.92
            1400      7.16      113.6      12.67
            1500      7.12      115.8      12.43

And the figure below displays them in graphical form.

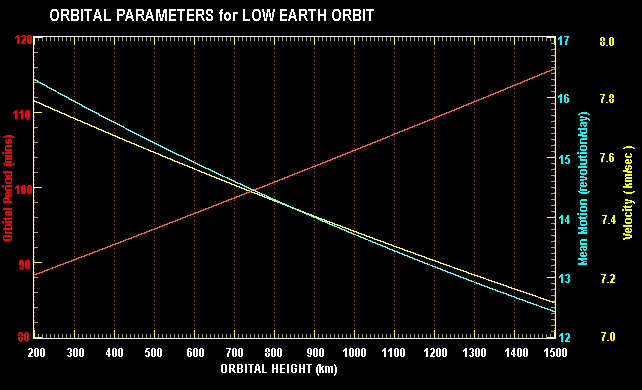
The red curve shows the orbital period in minutes, and its corresponding scale is on the left hand side of the graph. The right hand side scale is used for both the orbital velocity (yellow) which ranges in value from 7 to 8 km/sec, and the mean motion (blue) which varies from 12 to 17 orbits per day.

Australian Space Academy